2.3 Recursion - Đệ quy
Ý tưởng gọi một hàm từ bên trong một hàm khác lập tức gợi đến khả năng một hàm gọi chính nó. Cơ chế hàm gọi chính nó này được gọi là đệ quy. Đệ quy là một kĩ thuật lập trình quan trọng, là chìa khóa giải quyết nhiều ứng dụng tính toán cực kì quan trọng, từ các phương pháp tìm kiếm tổ hợp và sắp xếp để hỗ trợ xử lý thông tin cơ bản (Chương 4), cho đến phương pháp xử lý tín hiệu số Fast Fourier Transform for signal processing (Chương 9).
Chương trình đệ quy đầu tiên.
Chương trình HelloWorld cho đệ quy là hàm tính giai thừa factorial, nó tính giai thừa của các số nguyên dương N theo công thức:N! = N × (N-1) × (N-2) × ... × 2 × 1Ta có thể dễ dàng tính N! bằng một vòng for, nhưng cách đó vẫn chưa đơn giản bằng phương pháp trong Factorial.java đó là dùng hàm đệ quy sau đây:
Bạn có thể tự chứng minh rằng hàm đó cho kết quả mong muốn bằng cách để ý rằng factorial() trả về 1 = 1! khi N bằng 1 và nếu nó tính đúng giá trị
public static int factorial(int N) { if (N == 1) return 1; return N * factorial(N-1); }
(N-1)! = (N-1) × (N-2) × ... × 2 × 1thì nó cũng tính đúng giá trị
N! = N × (N-1)! = N × (N-1) × (N-2) × ... × 2 × 1Ta có thể lần bước quá trình tính toán đó theo cách ta vẫn lần bước các chuỗi lời gọi hàm.
factorial(5) factorial(4) factorial(3) factorial(2) factorial(1) return 1 return 2*1 = 2 return 3*2 = 6 return 4*6 = 24 return 5*24 = 120
Cài đặt hàm factorial() của ta có hai thành phần chính mà mỗi hàm đệ quy đều phải có.
- Trường hợp cơ bản (base case) trả về một giá trị mà không phải thực hiện thêm lời gọi đệ quy nào. Trường hợp cơ bản áp dụng cho một hoặc vài giá trị input đặc biệt mà khi đó hàm có thể tính giá trị mà không cần đệ quy. Với factorial(), trường hợp cơ bản là khi N = 1.
- Bước đệ quy (reduction step) là phần trung tâm của một hàm đệ quy. Nó mô tả mối quan hệ giữa hàm với một (hoặc nhiều) input hiện tại với hàm đó khi tính giá trị với một (hoặc nhiều) input khác. Ngoài ra, chuỗi các giá trị tham số phải hội tụ về trường hợp cơ bản. Với factorial(), bước đệ quy là N * factorial(N-1) và N giảm đi 1 với mỗi lần gọi hàm, do đó chuỗi các giá trị tham số hội tụ về trường hợp cơ bản N = 1.
Quy nạp toán học.
Lập trình đệ quy có quan hệ trực tiếp với quy nạp toán học, một kĩ thuật chứng minh áp dụng cho các hàm rời rạc. Việc dùng quy nạp để chứng minh một phát biểu về một số nguyên N là đúng cho vô hạn các giá trị N bao gồm hai bước.- Trường hợp cơ bản là chứng minh rằng phát biểu đó đúng với một vài giá trị nào đó của N (thường là 0 hoặc 1).
- Bước quy nạp là phần trung tâm của chứng minh. Ví dụ, ta thường giả thiết rằng phát biểu đúng với mọi số nguyên dương nhỏ hơn N, sau đó dùng dữ kiện đó để chứng minh rằng nó cũng đúng với N.
Thuật toán Euclid.
Ước số chung lớn nhất - greatest common divisor (gcd) của hai số nguyên dương là số nguyên lớn nhất mà cả hai số đó đều chia hết. Ví dụ, UCLN của 102 và 68 là 34, vì cả 102 và 68 đều là bội số của 34, nhưng không có số nào lớn hơn 34 mà cả hai cùng chia hết cho số đó.Ta có thể tính UCLN - gcd một cách rất hiệu quả nếu sử dụng tính chất sau đây của các số nguyên dương p và q:
Nếu p > q, thì UCLN(p,q) = UCLN(q, p % q).
Phương thức static gcd() trong Euclid.java là một hàm đệ quy ngắn gọn với bước đệ quy dựa vào tính chất trên.
gcd(1440, 408) gcd(408, 216) gcd(216, 192) gcd(192, 24) gcd(24, 0) return 24 return 24 return 24 return 24 return 24
Bài toán Tháp Hà Nội.
Một bài giảng về đệ quy không thể hoàn chỉnh nếu không nhăc đến bài toán cổ Tháp Hà Nội. Ta có ba cột và n đĩa có thể xếp lồng vào các cột đó. Các cái đĩa đó có kích thước khác nhau và ban đầu được xếp vào một cột trong số đó, theo thứ tự đĩa lớn bên dưới, đĩa nhỏ bên trên (đĩa n nằm dưới đáy và đĩa 1 trên đỉnh). Nhiệm vụ là di chuyển chồng đĩa sang một cột khác, tuân thủ các quy tắc sau:- Mỗi lần chỉ được di chuyển một đĩa.
- Không bao giờ đặt một đĩa lên trên một đĩa nhỏ hơn.
Để giải bài toán, mục tiêu của ta là tạo ra một chuỗi lệnh di chuyển đĩa. Giả sử các cột được xếp thành hàng, mỗi lệnh di chuyển đĩa quy định 2 thông tin: số hiệu đĩa cần di chuyển và hướng di chuyển (trái hay phải).
Với một đĩa nằm trên cột bên trái, lệnh chuyển sang trái có tác dụng xoay vòng chuyển nó sang cột bên phải; với một đĩa nằm trên cột phải, lệnh di chuyển sang phải sẽ xoay vòng chuyển nó sang cột bên trái.

Exponential time - thời gian chạy lũy thừa.
Một truyền thuyết nói rằng trong một ngôi đền có một nhóm các nhà sư ngồi giải bài toán Tháp Hà Nội với 64 cái đĩa bằng vàng trên ba chiếc kim bằng kim cương. Khi các nhà sư này giải xong thì ngày đó sẽ là ngày tận thế. Ta có thể ước lượng thời gian cho đến ngày tận thế đó (giả sử truyền thuyết kia đúng). Nếu ta định nghĩa hàm T(n) là số lệnh di chuyển mà chương trình TowersOfHanoi.java sinh ra để di chuyển n đĩa từ một cột sang một cột khác, thì hàm đệ quy cho thấy T(n) phải thỏa mãn hệ phương trình sau:T(n) = 2 T(n - 1) + 1 với n > 1, và T(1) = 1
Một hệ phương trình như vậy trong toán rời rạc được gọi là một quan hệ đệ quy - recurrence relation. Ta thường dùng chúng để rút ra một biểu thức dạng đóng là công thức cho một đại lượng quan tâm. Chẳng hạn, T(1) = 1, T(2) = 3, T(3) = 7, and T(4) = 15. Tổng quát, T(n) = 2^n - 1.
Khi biết giá trị của T(n), ta có thể ước lượng thời gian cần thiết để thực hiện tất cả các bước di chuyển. Nếu cứ mỗi giây, các nhà sư lại chuyển được một đĩa, họ sẽ cần 1 tuần để giải xong bài toán 20 đĩa, hơn 31 năm cho bài toán 30 đĩa, và hơn 348 thế kỉ cho một bài toán 40 đĩa (giả thiết rằng họ không di chuyển nhầm bước nào). Bài toán 64 đĩa sẽ cần đến hơn 5,8 tỷ thế kỷ.
Gray code - Mã Gray.
Nhà biên kịch Samuel Beckett đã viết một vở kịch có tên Quad với tính chất sau: Mở màn là một sân khấu trống rỗng, mỗi thời điểm chỉ có nhiều nhất 01 nhân vật vào hoặc ra sân khấu. Nhưng mỗi nhóm nhân vật xuất hiện trên sân khấu đúng 01 lần. Vở kịch có bốn nhân vật. Do đó có 2^4 = 16 nhóm nhân vật khác nhau, nghĩa là 16 tập con của tập hợp gồm 4 phần tử; Cái tên của vở kịch xuất phát từ đó. Hỏi Beckett làm thế nào để tạo ra hướng dẫn vào ra cho vở kịch này. Nếu số nhân vật là 5 hoặc nhiều hơn thì ta làm cách nào? (enter: ra sân khấu, exit: vào bên trong cánh gà - ra khỏi sân khấu).
| 
|
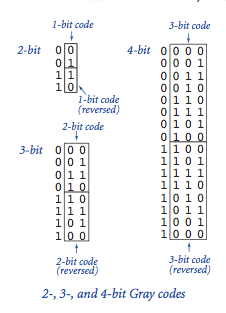
Mã Gray n-bit là một danh sách gồm 2^n số nhị phân n-bit khác nhau sao cho mỗi số trong danh sách đều khác số liền trước nó đúng 01 bit. Mã Gray áp dụng trực tiếp cho bài toán của Beckett vì ta có thể coi mỗi số nhị phân trong dãy đại diện cho một tập con của n phần tử, với mỗi bit đại diện cho việc số tự nhiên tương ứng với vị trí của bit đó có nằm trong tập con đó hay không. Việc thay đổi giá trị của một bit từ 0 đến 1 tương ứng với việc một số nguyên được đưa vào tập con; thay đổi từ 1 về 0 ứng với việc một số tự nhiên ra khỏi tập con.
Ta sinh mã Gray bằng cách nào? Một kế hoạch đệ quy khá tương tự với thuật toán đã dùng cho bài Tháp Hà Nội. Bộ số nhị phân n bit biểu diễn mã Gray được định nghĩa một cách đệ quy như sau:
- bộ mã n-1 bit, gắn thêm một bit 0 ở trước mỗi từ, tiếp theo là
- bộ mã n-1 bit, gắn thêm một bit 1 ở trước mỗi từ.
Recursive graphics - Đồ họa đệ quy.
Một thuật toán vẽ đệ quy đơn giản có thể đem lại một hình ảnh rất phức tạp. Ví dụ, một hình H-tree bậc n được định nghĩa như sau: Trường hợp cơ bản, n = 0, là hình rỗng không. Bước đệ quy là vẽ ba đoạn thẳng tạo thành hình chữ H trong phạm vi hình vuông đơn vị, và bốn hình H-tree bậc n-1 tại bốn đầu mút của chữ H vừa vẽ. Điều kiện bổ sung là các hình H-tree bậc n-1 nằm tại tâm của bốn mảng 1/4 của hình vuông nói trên, với kích thước giảm còn một nửa. Chương trình Htree.java nhận n là tham số dòng lệnh và vẽ một hình H-tree bậc n bằng thư viện StdDraw.

| 
| 
| 
| 
|
Brownian bridge - Cầu Brown.
H-tree là một ví dụ đơn giản của fractal: một hình hình học có thể chia thành các phần mà mỗi phần là (xấp xỉ) một bản sao thu nhỏ của hình ban đầu. Nghiên cứu về fractals đóng một vai trò quan trọng và dài lâu trong nghệ thuật, phân tích kinh tế, và các phát kiến khoa học. Các nghệ sỹ và nhà khoa học sử dụng fractal để xây dựng các mô hình xúc tích của các hình dạng phức tạp xuất hiện trong tự nhiên mà hình học truyền thống không thể mô tả được, chẳng hạn như mây, thực vật, núi, lưu vực sông, da người, và nhiều thứ khác. Các nhà kinh tế học cũng dùng fractal để mô hình hóa các đồ thị hàm số của các chỉ số kinh tế.Chương trình Brownian.java tạo một đồ thị hàm số xấp xỉ một ví dụ đơn giản được gọi là cây cầu Brown (Brownian bridge) và các hàm liên quan. Bạn có thể coi đồ thị này như là một đường nối ngẫu nhiên giữa hai điểm, từ (x0, y0) tới (x1, y1), được điều khiển bởi một số tham số. Cài đặt này dựa trên phương pháp thay điểm giữa (midpoint displacement method), đó là một thuật toán đệ quy cho việc vẽ đồ thị trong khoảng [x0, x1]. Trường hợp cơ bản (khi độ dài của khoảng nhỏ hơn một ngưỡng chấp nhận cho trước) là vẽ một đoạn thẳng nối hai điểm. Bước đệ quy là chia khoảng quan tâm làm đôi, quy trình như sau:
- tính trung điểm (xm, ym) của khoảng đang xét.
- Cộng vào tọa độ y của trung điểm một giá trị ngẫu nhiên δ, lấy từ phân bố Gauss với kì vọng bằng 0 và một variance cho trước.
- Đệ quy cho các đoạn con, chia variance theo một hệ số tỷ lệ s cho trước .
Đường cong được điều khiển bởi hai tham số: volatility (giá trị ban đầu của variance) điều khiển khoảng cách tối đa của đồ thị tới đường thẳng nối hai điểm, và Hurst exponent điều khiển độ mịn của đường cong. Ta kí hiệu Hurst exponent bằng H và chia variance cho 2^(2H) tại mỗi tầng đệ quy. Khi H bằng 1/2 (nghĩa là chia đôi ở mỗi tầng) độ lệch chuẩn sẽ là một hằng số đối với toàn bộ đường cong: trong trường hợp này, đường cong là một đường dạng cầu Brown.
Các lỗi thường gặp khi dùng đệ quy.
Với đệ quy, bạn có thể viết những chương trình đẹp và ngắn gọn mà khi chạy nó lại thất bại thảm hại.- Thiếu trường hợp cơ bản.
Hàm đệ quy trong
NoBaseCase.java
có nhiệm vu tính các số điều hòa (Harmonic), nhưng nó thiếu một trường hợp cơ bản:
Khi bạn gọi hàm này, nó sẽ gọi đi gọi lại chính nó và không bao giờ trả về.public static double H(int N) { return H(N-1) + 1.0/N; } - Không đảm bảo hội tụ.
Một lỗi khác là đặt vào trong hàm đệ quy một lời gọi đệ quy cho một bài toán con không giảm kích thước.
Hàm đệ quy trong
NoConvergence.java
sẽ lặp vô tận nếu nó được gọi với một tham số khác 1:
public static double H(int N) { if (N == 1) return 1.0; return H(N) + 1.0/N; } - Quá tốn bộ nhớ.
Mỗi lời gọi hàm cần được lưu lại dấu vết trong bộ nhớ (ngăn xếp các lời gọi hàm - function call stack), các lời gọi hàm đệ quy không phải ngoại lệ. Nếu một hàm gọi chính nó quá nhiều lần trước khi trả về, không gian bộ nhớ cần thiết cho việc lưu lại các lời gọi hàm đó có thể vượt quá lượng bộ nhớ cho phép.
Hàm đệ quy trong
ExcessiveSpace.java
tính đúng số harmonic thứ N. Tuy nhiên, ta không thể dùng hàm đó cho các giá trị N lớn, vì độ sâu đệ quy tỷ lệ thuận với N, và khi N đạt giá trị 5000, chương trình sẽ gây lỗi StackOverflowError - tràn bộ nhớ stack.
public static double H(int N) { if (N == 0) return 0.0; return H(N-1) + 1.0/N; }
- Tính đi tính lại quá nhiều.
Khi viết một chương trình đệ quy đơn giản, cần cẩn thận lưu ý rằng một chương trình đơn giản có thể đòi hỏi thời gian chạy cấp lũy thừa (một cách không cần thiết) do việc tính đi tính lại quá nhiều.
Ví dụ, chuỗi Fibonacci
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 ...
được định nghĩa bằng công thức Fn = Fn-1 + Fn-2 với n ≥ 2 và F0 = 0 và F1 = 1. Một lập trình viên thiếu kinh nghiệm có thể cài hàm đệ quy sau để tính các số trong một chuỗi Fibonacci, như trong Fibonacci.java:
Tuy nhiên, chương trình trên cực kì không hiệu quả! Để thấy vì sao làm như trên lại không hiệu quả, hãy xét cách hàm trên tính F(8) = 21. Đầu tiên, nó tính F(7) = 13 và F(6) = 8. Để tính F(7), nó gọi đệ quy tính F(6) = 8 một lần nữa và F(5) = 5. Tình hình nhanh chóng trở nên ngày càng tồi tệ, vì trong cả hai lần tính F[6] nó đều bỏ qua thực tế là F(5) đã được tính rồi, và cứ như vậy. Khi tính F(n), số lần chương trình này tính F(1) chính bằng Fn. Lỗi tính đi tính lại này tăng lên theo cấp lũy thừa. Không có một cái máy tính nào, kể cả viễn tưởng, có thể tính được nhiều như vậy.public static long F(int n) { if (n == 0) return 0; if (n == 1) return 1; return F(n-1) + F(n-2); }
Q + A
Q. Có khi nào vòng lặp là cách duy nhất để giải một bài toán?
A. Không, bất cứ vòng lặp nào cũng có thể thay thế bằng một hàm đệ quy, tuy nhiên phiên bản đệ quy có thể đòi hỏi quá nhiều bộ nhớ.
Q. Có khi nào đệ quy là cách duy nhất để giải một bài toán?
A. Không, hàm đệ quy bất kì đều có thể thay thế bằng một phiên bản dùng vòng lặp. Ở mục 4.3, ta sẽ thấy cách trình biên dịch sinh mã cho các lời gọi hàm bằng cách sử dụng một cấu trúc dữ liệu gọi là stack.
Q. Tôi nên ưu tiên chọn cái gì hơn, đệ quy hay vòng lặp?
A. Hãy chọn cách nào cho bạn code đơn giản dễ hiểu hơn, hoặc hiệu quả hơn.
Q. Tôi lo ngại về việc mã đệ quy dùng quá nhiều bộ nhớ và tính toán lại quá nhiều lần. Ngoài ra còn nên để ý những vấn đề gì nữa không?
A. Cực kì cẩn trọng trong việc tạo mảng trong mã đệ quy. Lượng bộ nhớ sử dụng có thể tăng lên rất rất nhanh, cũng như thời gian tiêu tốn cho việc quản lý phần bộ nhớ đó.
Bài tập
- Chuyện gì xảy ra nếu bạn chạy factorial() với giá trị n âm? với giá trị lớn, chẳng hạn 35?
- Viết một chương trình đệ quy tính giá trị ln(N!).
-
Tìm dãy số nguyên in ra bởi lời gọi hàm ex233(6):
public static void ex233(int n) { if (n <= 0) return; StdOut.println(n); ex233(n-2); ex233(n-3); StdOut.println(n); } -
Tìm giá trị trả về của hàm ex234(6):
public static String ex234(int n) { if (n <= 0) return ""; return ex234(n-3) + n + ex234(n-2) + n; } -
Phân tích nhược điểm của hàm đệ quy:
public static String ex235(int n) { String s = ex233(n-3) + n + ex235(n-2) + n; if (n <= 0) return ""; return s; } - Cho bốn số nguyên dương a, b, c, và d, giải thích giá trị kết quả của lời gọi gcd(gcd(a, b), gcd(c, d)).
-
Giải thích hoạt động của hàm tựa Euclid sau bằng các khái niệm số nguyên và ước số.
public static boolean gcdlike(int p, int q) { if (q == 0) return (p == 1); return gcdlike(q, p % q); }Lời giải. Kiểm tra xem p và q có nguyên tố cùng nhau hay không.
-
Xét hàm đệ quy sau.
public static int mystery(int a, int b) { if (b == 0) return 0; if (b % 2 == 0) return mystery(a+a, b/2); return mystery(a+a, b/2) + a; }mystery(2, 25) và mystery(3, 11) trả về kết quả gì? Cho các số nguyên dương a và b, hàm mystery(a, b) tính cái gì? Câu hỏi tương tự, nhưng thay + bằng * và thay return 0 bằng return 1.
Đáp án. 50 và 33. Nó tính a*b. Nếu thay + bằng *, thì nó tính a^b.
- Viết chương trình đệ quy Ruler.java với nhiệm vụ vẽ các vạch chia của một thước kẻ, sử dụng thư viện StdDraw.
-
Solve the following recurrence relations, all with T(1) = 1. Assume N
is a power of two.
- T(N) = T(N/2) + 1
- T(N) = 2T(N/2) + 1
- T(N) = 2T(N/2) + N
- T(N) = 4T(N/2) + 3
- Dùng quy nạp chứng minh rằng lời giải đệ quy của ta cho kết quả là số lệnh di chuyển tối thiểu.
- Prove by induction that the recursive program given in the text makes exactly F(n) recursive calls to F(1) when computing F(N).
- Chứng minh rằng cứ sau 2 lời gọi đệ quy thì đối số thứ hai của gcd() giảm ít nhất một nửa. Sau đó, chứng minh rằng gcd(p, q) dùng tối đa log2 N lời gọi đệ quy, với N là giá trị lớn hơn trong hai giá trị p và q.
-
Viết chương trình AnimatedHtree.java vẽ hoạt hình xây dựng hình H-tree.
Sau đó, sắp xếp lại trật tự của các lời gọi đệ quy (và trường hợp cơ bản), xem kết quả hoạt hình sau đó, và giải thích kết quả.
Creative Exercises
- Binary representation. Biểu diễn nhị phân Viết chương trình IntegerToBinary.java lấy tham số dòng lệnh là số nguyên dương N (hệ thập phân) và in ra biểu diễn nhị phân của nó. Thay vì dùng phương pháp tách dần các lũy thừa của 2. Ta hãy dùng cách đơn giản hơn: chia N cho 2 lấy phần dư và in ngược thứ tự. Đầu tiên hãy thử dùng một vòng while để thực hiện tính toán và in các bit ra - sẽ là thứ tự ngược. Sau đó sửa lại, dùng đệ quy để in các bit đó theo đúng thứ tự.
- A4 paper. Tỷ lệ chiều rộng-chiều cao của trang giấy theo chuẩn ISO là 1 trên căn 2. Định dạng A0 có diện tích 1 m vuông. A1 là A0 chia đôi bằng một đường thẳng, A2 là A1 chia đôi bằng một đường thẳng, cứ như vậy. Hãy viết một chương trình nhận n là tham số dòng lệnh và dùng thư viện StdDraw để thể hiện cách cắt một tờ giấy khổ A0 thành 2^n mảnh. Đây là một minh họa về các khổ giấy loại A.
- Permutations. - Hoán vị
Viết một chương trình Permutations.java
lấy một tham số dòng lệnh n và in ra tất cả n! hoán vị của n chữ cái bắt đầu từ a (giả sử n không lớn hơn 26).
Một hoán vị của n phần tử là một trong n! thứ tự có thể có của các phần tử đó.
Ví dụ, với n = 3, bạn cần ra được output sau: không cần quan tâm thứ tự liên kê các hoán vị đó.
bca cba cab acb bac abc
- Các hoán vị độ dài k.
Sửa Permutations.java thành
PermutationsK.java sao cho chương trình mới lấy hai tham số dòng lệnh n và k, và in ra tất cả
P(n, k) = n! / (n-k)! hoán vị chứa đúng k trong n phần tử.
Dưới đây là output khi k = 2 và n = 4.
Bạn có thể in ra theo thứ tự bất kì.
ab ac ad ba bc bd ca cb cd da db dc
- Combinations - tổ hợp.
Viết chương trình Combinations.java
that takes one command-line argument n and prints out all 2^n
combinations of any size. A combination is a subset of the
n elements, independent of order.
As an example, when n = 3 you should get the following output.
Note that the first element printed is the empty string (subset of size 0).a ab abc ac b bc c
- Combinations of size k.
Modify Combinations.java to
CombinationsK.java so that
it takes two command-line arguments n and k, and prints out all
C(n, k) = n! / (k! * (n-k)!) combinations of size k.
For example, when n = 5 and k = 3 you should get the following output.
Alternate solution using arrays instead of strings: Comb2.java.abc abd abe acd ace ade bcd bce bde cde
- Hamming distance.
The Hamming distance between two bit strings of length n is equal
to the number of bits in which the two strings differ.
Write a program that reads in an integer k and a bit string s
from the command line, and prints out all bit strings that
have Hamming distance at most k from s. For example if
k is 2 and s is 0000 then your program should print out
Hint: choose k of the N bits in s to flip.0011 0101 0110 1001 1010 1100
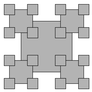
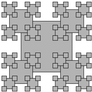
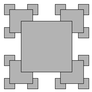
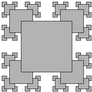
- Recursive squares.
Write a program to produce each of the following recursive patterns.
The ratio of the sizes of the squares is 2.2.
To draw a shaded square, draw a filled gray square, then an
unfilled black square.
RecursiveSquares.java gives a solution to part a.
-
- Pancake flipping. You have a stack of N pancakes of varying sizes on a griddle. Your goal is to re-arrange the stack in descending order so that the largest pancake is on the bottom and the smallest one is on top. You are only permitted to flip the top k pancakes, thereby reversing their order. Devise a scheme to arrange the pancakes in the proper order by using at most 2N - 3 flips. Hint: you can try out strategies here.
- Gray code.
Modify Beckett.java to print out the
Gray code (not just the sequence of bit positions that change).
Solution. GrayCode.java uses Java's string data type; GrayCodeArray.java uses a boolean array.
- Towers of Hanoi variant. Consider the following variant of the towers of Hanoi problem. There are 2N discs of increasing size stored on three poles. Initially all of the discs with odd size (1, 3, ..., 2N-1) are piled on the left pole from top to bottom in increasing order of size; all of the discs with even size (2, 4, ..., 2N) are piled on the right pole. Write a program to provide instructions for moving the odd discs to the right pole and the even discs to the left pole, obeying the same rules as for towers of Hanoi.
- Animated towers of Hanoi animation. Write a program AnimatedHanoi.java that uses StdDraw to animate a solution to the towers of Hanoi problem, moving the discs at a rate of approximately 1 per second.
- Sierpinski triangles.
Write a recursive program to draw the Sierpinski gasket.
As with Htree, use a command-line argument to control the
depth of recursion.








- Binomial distribution.
Estimate the number of recursive calls that would be used
by the code
to compute binomial(100, 50). Develop a better implementation that is based on memoization. Hint: See Exercise 1.4.26.public static double binomial(int N, int k) { if ((N == 0) || (k < 0)) return 1.0; return (binomial(N-1, k) + binomial(N-1, k-1)) / 2.0; } - Collatz function.
Consider the following recursive function in
Collatz.java, which is related
to a famous unsolved problem in number theory, known as the
Collatz problem or the 3n + 1 problem.
public static void collatz(int n) { StdOut.print(n + " "); if (n == 1) return; if (n % 2 == 0) collatz(n / 2); else collatz(3*n + 1); }For example, a call to collatz(7) prints the sequence
7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
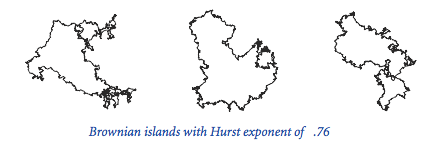
as a consequence of 17 recursive calls. Write a program that takes a command-line argument N and returns the value of n < N for which the number of recursive calls for collatz(n) is maximized. Hint: use memoization. The unsolved problem is that no one knows whether the function terminates for all positive values of n (mathematical induction is no help because one of the recursive calls is for a larger value of the argument). - Brownian island. Benoit Mandelbrot asked the famous question
How long is the coast of Britain?
Modify Brownian.java to get a program
BrownianIsland.java
that plots
Brownian islands,
whose coastlines resemble that of Great Britain. The modifications are simple:
first, change curve() to add a gaussian to the x coordinate as well
as to the y coordinate;
second, change main() to draw a curve from the point at the center of the
canvas back to itself. Experiment with various values of the arguments to
get your program to produce islands with a realistic look.
- Plasma clouds. Write a recursive program Program PlasmaCloud.java to draw plasma clouds, using the method suggested in the text. Remark: this technique can be used to produce synthetic terrain, by interpreting the color value as the altitude. Variants of this scheme are widely used in the entertainment industry to generate artificial background scenery for movies and the "Genesis effect" in Star Trek II and the "outline of the "Death Star" in Return of the Jedi.
- A strange function.
Consider McCarthy's 91 function:
public static int mcCarthy(int n) { if (n > 100) return n - 10; else return mcCarthy(mcCarthy(n+11)); }Determine the value of mcCarthy(50) without using a computer. Give the number of recursive calls used by mcCarthy() to compute this result. Prove that the base case is reached for all positive integers n or give a value of n for which this function goes into a recursive loop.
- Recursive tree.
Write a program Tree.java
that takes a command-line arguemnt N and produces the following
recurisve patterns for N equal to 1, 2, 3, 4, and 8.

Web Exercises
- Does Euclid.java still work if the inputs can be negative? If not, fix it. Hint: Recall that % can return a negative integer if the first input is negative. When calling the function, take the absolute value of both inputs.
-
Write a recursive
program GoldenRatio.java that
takes an integer input N and computes
an approximation to the
golden ratio
using the following recursive formula:
Redo, but do not use recursion.f(N) = 1 if N = 0 = 1 + 1 / f(N-1) if N > 0 - Discover a connection between the golden ratio and Fibonacci numbers. Hint: consider the ratio of successive Fibonacci numbers: 2/1, 3/2, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
-
Consider the following recursive function. What is
mystery(1, 7)?
public static int mystery(int a, int b) { if (0 == b) return 0; else return a + mystery(a, b-1); }Will the function in the previous exercise terminate for every pair of integers a and b between between 0 and 100? Give a high level description of what mystery(a, b) returns, given integers a and b between 0 and 100.
Answer: mystery(1, 7) = 1 + mystery(1, 6) = 1 + (1 + mystery(1, 5)) = ... 7 + mystery(1, 0) = 7.
Answer: Yes, the base case is b = 0. Successive recursive calls reduce b by 1, driving it toward the base case. The function mystery(a, b) returns a * b. Mathematically inclined students can prove this fact via induction using the identity ab = a + a(b-1).
-
Consider the following function. What does mystery(0, 8) do?
Answer: infinite loop.public static void mystery(int a, int b) { if (a != b) { int m = (a + b) / 2; mystery(a, m); StdOut.println(m); mystery(m, b); } } -
Consider the following function. What does mystery(0, 8) do?
Answer: stack overflow.public static void mystery(int a, int b) { if (a != b) { int m = (a + b) / 2; mystery(a, m - 1); StdOut.println(m); mystery(m + 1, b); } } - Repeat the previous exercise, but replace if (a != b) with if (a <= b).
-
What does mystery(0, 8) do?
public static int mystery(int a, int b) { if (a == b) StdOut.println(a); else { int m1 = (a + b ) / 2; int m2 = (a + b + 1) / 2; mystery(a, m1); mystery(m2, b); } } -
What does the following function compute?
public static int f(int n) { if (n == 0) return 0; if (n == 1) return 1; if (n == 2) return 1; return 2*f(n-2) + f(n-3); -
Write a program Fibonacci2.java
that takes a command-line argument N and prints out the first N
Fibonacci numbers using the following alternate definition:
F(n) = 1 if n = 1 or n = 2 = F((n+1)/2)2 + F((n-1)/2)2 if n is odd = F(n/2 + 1)2 - F(n/2 - 1)2 if n is evenWhat is the biggest Fibonacci number you can compute in under a minute using this definition? Compare this to Fibonacci.java.
-
Write a program
that takes a command-line argument N and prints out the first N
Fibonacci numbers using the
following
method proposed by Dijkstra:
F(0) = 0 F(1) = 1 F(2n-1) = F(n-1)^2 + F(n)^2 F(2n) = (2F(n-1) + F(n)) * F(n)
- Prove by mathematical induction that the alternate definitions of the Fibonacci function given in the previous two exercises are equivalent to the original definition.
- Write a program Pell.java that takes a command-line argument N and prints out the first N Pell numbers: p0 = 0, p1 = 1, and for n >= 2, pn = 2 pn-1 + pn-2. Print out the ratio of successive terms and compare to 1 + sqrt(2).
-
Consider the following function from program
Recursion.java:
public static void mystery(int n) { if (n == 0 || n == 1) return; mystery(n-2); StdOut.println(n); mystery(n-1); }What does mystery(6) print out? Hint: first figure out what mystery(2), mystery(3), and so forth print out.
-
What would happen in the previous exercise if the base case
was replaced with the following statement?
if (n == 0) return;
-
Consider the following recursive functions.
public static int square(int n) { if (n == 0) return 0; return square(n-1) + 2*n - 1; } public static int cube(int n) { if (n == 0) return 0; return cube(n-1) + 3*(square(n)) - 3*n + 1; }What is the value of square(5)? cube(5)? cube(123)?
-
Consider the following pair of mutually recursive functions.
What does g(g(2)) evaluate to?
public static int f(int n) { public static int g(int n) { if (n == 0) return 0; if (n == 0) return 0; return f(n-1) + g(n-1); return g(n-1) + f(n); } } - Write program to verify that (for small values of n) the sum of the cubes of the first n Fibonacci numbers F(0)^3 + F(1)^3 + ... + F(n)^3 equals (F(3n+4) + (-1)^n * 6 * f(n-1)) / 10, where F(0) = 1, F(1) = 1, F(2) = 2, and so forth.
- Transformations by increment and unfolding.
Given two integers a ≤ b, write a program
Sequence.java
that transforms a into b by a minimum
sequence of increment (add 1) and unfolding (multiply by 2) operations.
For example,
% java Sequence 5 23 23 = ((5 * 2 + 1) * 2 + 1) % java Sequence 11 113 113 = ((((11 + 1) + 1) + 1) * 2 * 2 * 2 + 1)
- Hadamard matrix.
Write a recursive program Hadamard.java that
takes a command-line argument n and plots an N-by-N Hadamard pattern where
N = 2n.
Do not use an array.
A 1-by-1 Hadamard pattern is a single black square.
In general a 2N-by-2N Hadamard pattern is obtained by aligning 4 copies
of the N-by-N pattern in the form of a 2-by-2 grid, and then
inverting the colors of all the squares in the lower right N-by-N copy.
The N-by-N Hadamard H(N) matrix is a boolean matrix with the remarkable
property that any two rows differ in exactly N/2 bits.
This property makes it useful for designing error-correcting codes.
Here are the first few Hadamard matrices.




- 8 queens problem.
In this exercise, you will solve the classic
8-queens problem: place 8
queens on an 8x8 chess board so that no two queens are in the same row,
column, or diagonal. There are 8! = 40,320 ways in which no two queens are
placed in the same row or column. Any permutation p[] of the integers
0 to 7 gives such a placement: put queen i in row i, column p[i].
Your program Queens.java should take
one command-line argument N and enumerate all solutions to the
N-queens problem by drawing the location of the queens in ASCII like
the two solutions below.
Hint: to determine whether setting q[n] = i conflicts with q[0] through q[n-1]* * * Q * * * * * * * * Q * * * * Q * * * * * * * Q * * * * * * * * * * * * Q * * * * Q * * * * * * Q * * * * * * * * * * * Q * * * * * * Q * * * * Q * * * * * * * * * * * * Q * * * * * * * Q * * * * Q * * * * * * * * Q * * Q * * * * * * * Q * * * * * * *
- if q[i] equals q[n]: two queens are placed in the same column
- if q[i] - q[n] equals n - i: two queens are on same major diagonal
- if q[n] - q[i] equals n - i: two queens are on same minor diagonal
- Another 8 queens solver. Program Queens2.java solves the 8 queens problem by implicitly enumeration all N! permutations (instead of the N^N placements). It is based on program Permutations.java.
- Euclid's algorithm and π. The probability that two numbers chosen from a large random set of numbers have no common factors (other than 1) is 6 / π2. Use this idea to estimate π. Robert Matthews use the same idea to estimate π by taken the set of numbers to be a function of the positions of stars in the sky.
- Towers of Hanoi variant II. (Knuth-Graham and Pathashnik) Solve the original Towers of Hanoi problem, but with the extra restriction that you are not allowed to directly transfer a disk from A to C. How many moves does it take to solve a problem with N disks? Hint: move N-1 smallest disks from A to C recursively (without any direct A to C moves), move disk N from A to B, move N-1 smallest disks from C to A (without any direct A to C moves), move disk N from B to C, and move N-1 smallest disks from A to C recursively (without any direct A to C moves).
- Towers of Hanoi variant III. Repeat the previous question but disallow both A to C and C to A moves. That is, each move must involve pole B.
- Towers of Hanoi with 4 pegs. Suppose that you have a fourth peg. What is the least number of moves needed to transfer a stack of 8 disks from the leftmost peg to the rightmost peg? Answer. Finding the shortest such solution in general has remained an open problem for over a hundred years and is known as Reve's puzzle.
-
Another tricky recursive function.
Consider the following recursive function.
What is f(0)?
public static int f(int x) { if (x > 1000) return x - 4; else return f(f(x+5)); } - Checking if N is a Fibonacci number. Write a function to check if N is a Fibonacci number. Hint: a positive integer is a Fibonacci number if and only if either (5*N*N + 4) or (5*N*N - 4) is a perfect square.
- Random infix expression generator.
Run Expr.java
with different command-line argument p between 0 and 1.
What do you observe?
public static String expr(double p) { double r = Math.random(); if (r <= 1*p) return "(" + expr(p) + " + " + expr(p) + ")"; if (r <= 2*p) return "(" + expr(p) + " * " + expr(p) + ")"; return "" + (int) (100 * Math.random()); } - A tricky recurrence.
Define F(n) so that F(0) = 0 and F(n) = n - F(F(n-1)).
What is F(100000000)?
Solution: The answer is related to the Fibonacci sequence and the Zeckendorf representation of a number.
- von Neumann ordinal.
The von Neumann integer i is defined as follows: for i = 0, it is the
empty set; for i > 0, it is the set containing the von Neumann integers 0 to i-1.
Write a program Ordinal.java with a recursive function vonNeumann() that takes a nonnegative integer N and returns a string representation of the von Neumann integer N. This is a method for defining ordinals in set theory.0 = {} = {} 1 = {0} = {{}} 2 = {0, 1} = {{}, {{}}} 3 = {0, 1, 2} = {{}, {{}}, {{}, {{}}}} - Subsequences of a string.
Write a program Subsequence.java
that takes a string command-line argument s and an integer
command-line argument k and prints out all subsequences
of s of length k.
% java Subsequence abcd 3 abc abd acd bcd
- Interleaving two strings.
Given two strings s and t of distinct characters,
print out all (M+N)! / (M! N!) interleavings, where M and N are the
number of characters in the two strings.
For example, if
s = "ab" t = "CD" abCD CabD aCbD CaDb aCDb CDab
- Binary GCD.
Write a program BinaryGCD.java
that finds the greatest common divisor of two positive integers
using the
binary gcd algorithm: gcd(p, q) =
- p if q = 0
- q if p = 0
- 2 * gcd(p/2, q/2) if p and q are even
- gcd(p/2, q) if p is even and q is odd
- gcd(p, q/2) if p is odd and q is even
- gcd((p-q)/2, q) if p and q are odd and p >= q
- gcd(p, (q-p)/2) if p and q are odd and p < q
- Integer partitions.
Write a program Partition.java
that takes a positive integer N as a command-line argument and
prints out all partitions of N.
A partition
of N is a way to write N as a sum of positive integers.
Two sums are considered the same if they only differ in the
order of their constituent summands.
Partitions arise in symmetric polynomials and group
representation theory in mathematics and physics.
% java Partition 4 % java Partition 6 4 6 3 1 5 1 2 2 4 2 2 1 1 4 1 1 1 1 1 1 3 3 3 2 1 3 1 1 1 2 2 2 2 2 1 1 2 1 1 1 1 1 1 1 1 1 1 - Johnson-Trotter permutations.
Write a program JohnsonTrotter.java
that take a command-line argument n and prints out all n! permutations
of the integer 0 through n-1 in such a way that consecutive permutations
differ in only one adjacent transposition (similar to way Gray code
iterates over combinations in such a way that consecutive combinations
differ in only one bit).
% java JohnsonTrotter 3 012 (2 1) 021 (1 0) 201 (2 1) 210 (0 1) 120 (1 2) 102 (0 1)
- Permutations in lexicographic order.
Write a program PermutationsLex.java
that take a command-line argument N and prints out all N! permutations
of the integer 0 through N-1 in lexicographic order.
% java PermutationsLex 3 012 021 102 120 201 210
- Derangements. A derangement is a permutation p[] of the integers from 0 to N-1 such that p[i] doesn't equal i for any i. For example there are 9 derangmenets when N = 4: 1032, 1230, 1302, 2031, 2301, 2310, 3012, 3201, 3210. Write a program to count the number of derangements of size N using the following recurrence: d[N] = (N-1) (d[N-1] + d[N-2]), where d[1] = 0, d[2] = 1. The first few terms are 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, and 1334961.
- Tribonacci numbers. The tribonacci numbers are similar to the Fibonacci numbers, except that each term is the sum of the three previous terms in the sequence. The first few terms are 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81. Write a program to compute tribonacci numbers. What is the ratio successive terms? Answer. Root of x^3 - x^2 - x - 1, which is approximately 1.83929.
- Sum of first n Fibonacci numbers. Prove by induction that the sum of the first n Fibonacci numbers F(1) + F(2) + ... + F(N) is F(N+2) - 1.
- Combinational Gray Code. Print out all combination of k of n items in such a way that consecutive combinations differ in exactly one element, e.g., if k = 3 and n = 5, 123, 134, 234, 124, 145, 245, 345, 135, 235, 125. Hint: use the Gray code, but only print out those integers with exactly k 1's in their binary representation.
- Maze generation. Create a maze using divide-and-conquer: Begin with a rectangular region with no walls. Choose a random gridpoint in the rectangle and construct two perpendicular walls, dividing the square into 4 subregions. Choose 3 of the four regions at random and open a one cell hole at a random point in each of the 3. Recur until each subregion has width or height 1.
- Plasma clouds.
Program PlasmaCloud.java
takes a command-line argument N and produces a random
N-by-N plasma fractal using the midpoint displacement method.



Here's an 800-by-800 example. Here's a reference, including a simple 1D version. Note: some visual artifacts are noticeable parallel to the x and y axes. Doesn't have all of the statistical properties of 2D fractional Brownian motion.
- Fern fractal. Write a recursive program to draw a fern or tree, as in this fern fractal demo.
- Integer set partition. Use memoization to develop a program that solves the set partition problem for positive integer values. You may use an array whose size is the sum of the input values.
- Voting power. John F. Banzhaf III proposed a ranking system for each coalition in a block voting system. Suppose party i control w[i] votes. A strict majority of the votes is needed to accept or reject a proposal. The voting power of party i is the number of minority coalitions it can join and turn it into a winning majority coalition. Write a program VotingPower.java that takes in a list of coalition weights as command-line argument and prints out the voting power of each coalition. Hint: use Schedule.java as a starting point.
- Scheduling on two parallel machines. Program Schedule.java takes a command-line argument N, reads in N real number of standard input, and partitions them into two groups so that their difference is minimized.


.png)