3.2   Creating Data Types

Tóm tắt.

Stopwatch.

Đây là phiên bản đơn giản của một đồng hồ bấm giờ loại cổ. Khi bạn tạo một đối tượng StopWatch, nó bắt đầu chạy, và bạn có thể hỏi xem nó đã chạy bao lâu rồi bằng cách gọi hàm elapsedTime().

Histogram.

Turtle graphics.

• Ngon. Chương trình Ngon.java lấy tham số dòng lệnh N và vẽ một đường N-gon chuẩn.

  với N đủ lớn, ta sẽ thu được xấp xỉ tốt cho một đường tròn. Trong hình học Đề-các, một đường tròn là quỹ tích của các điểm có khoảng cách r tới một điểm cố định (a, b). Công thức mô tả các điểm trên đường tròn:

  (x - a)^2 + (y - b)^2 = r^2

  Trong hình học giải tích, một đường tròn là đường cong có độ cong là hằng số: Công thức imperative mô tả cách vẽ.

  REPEAT GO FORWARD 1 UNIT TURN LEFT 1 UNIT

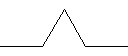
• Đường cong Koch. Đường Koch bậc 0 là một đoạn thẳng. Để vẽ đường Koch bậc n trong turtle graphics
  • Draw a Koch curve of order n-1 (Vẽ một đường Koch bậc n-1)
  • Rotate 60° counterclockwise (Xoay 60° ngược chiều kim đồng hồ)
  • Draw a Koch curve of order n-1 (Vẽ một đường Koch bậc n-1)
  • Rotate 120° clockwise (Xoay 120° theo chiều kim đồng hồ)
  • Draw a Koch curve of order n-1 (Vẽ một đường Koch bậc n-1)
  • Rotate 60° counterclockwise (Xoay 60° ngược chiều kim đồng hồ)
  • Draw a Koch curve of order n-1 (Vẽ một đường Koch bậc n-1)

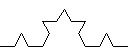
  Dưới đây là các đường Koch bậc 0, 1, 2, và 3.

  Chương trình Koch.java đọc tham số dòng lệnh N và vẽ một họa tiết dạng bông tuyết bậc N bằng thư viện của ta. Nó dùng một chút kiến thức hình học từ chương trình cấp 3 để tính kích thước cần vẽ cho các đoạn thẳng và tính xem bắt đầu vẽ chúng ở vị trí nào.

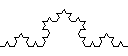
  Hoàn cảnh lịch sử: năm 1872 Karl Weierstrass có một phát kiến chấn động: một hàm liên tục nhưng không thể tính vi phân tại bất cứ điểm nào. Về sau, đó trở thành một trong những đặc điểm của fractal. Helge von Koch muốn tìm một ví dụ cụ thể hơn. Năm 1904, von Koch mô tả một cách dựng hình mà nay ta gọi là đường cong Koch. Von Koch chứng minh rằng, họa tiết bông tuyết của Koch là một đường cong vô hạn nhưng không có tiếp tuyến tại bất cứ điểm nào. Từ đó, ông chứng minh rằng tồn tại các hàm f(t) và g(t) sao cho đường Koch snowflake có công thức (f(t), g(t)) với 0 ≤ t ≤ 1, nhưng f(t) và g(t) là các hàm không thể tính vi phân.

• Spira mirabilis. Spiral.java tạo một đường xoắn ốc logarit. Nguyên lý sinh học: khi kích thước tăng, hình dạng không đổi. Đường kính tăng theo hàm lũy thừa của góc.

  

  Đường xoắn ốc logarit do Đề-các mô tả năm 1638. Bernouilli ấn tượng về các tính chất của nó đến mức ông đặt tên cho nó là Spira mirabilis (đường xoắn ốc kì diệu và tuyệt vời) và yêu cầu khắc nó lên bia mộ mình (nhưng người ta lại khắc đường xoắn ốc Ac-si-mét). Trong tự nhiên có các hình dạng này: vỏ ốc biển, tay của bão nhiệt đới, các nhánh của thiên hà xoắn ốc, đường bay của diều hâu khi tiếp cận mồi, hạt tích điện di chuyển trong một từ trường đều.

       

• Chuyển động Brown. Hình dung một con rùa mất phương hướng (theo dõi kiểu xoay và bước của nó) xoay theo một hướng ngẫu nhiên trước khi bước mỗi bước. DrunkenTurtle.java vẽ đường đi của con rùa đó. Năm 1827, nhà sinh vật học Robert Brown quan sát qua kính hiển vi một hạt phấn hoa chìm trong nước có vẻ di chyển theo một kiểu ngẫu nhiên như vậy, chuyển động này về sau được gọi là chuyển động Brown và dẫn đến lý thuyết của Albert Einstein về bản chất nguyên tử của vật chất. DrunkenTurtles.java vẽ nhiều con rùa như vậy, tất cả đều lang thang không có phương hướng.

Complex numbers. - Số phức

Việc phát triển một kiểu dữ liệu cho các số phức là một ví dụ kinh điển về giá trị của lập trình hướng đối tượng. Không có ngôn ngữ lập trình nào có thể cung cấp cài đặt tất cả các trừu tượng toán học mà ta có thể cần đến, nhưng khả năng cài đặt các cấu trúc dữ liệu cho ta không chỉ khả năng viết chương trình để dễ dàng xử lý các cấu trúc như số phức, đa thức, vector, ma trận và nhiều công cụ cơ bản khác mà các nhà toán học đã phát triển trong các thế kỉ trở lại đây, mà còn là sự tự do tư duy theo ngôn ngữ của các trừu tượng hóa mới.

Các phép toán cơ bản đối với số phức là cộng (add) và nhân(multiply) áp dụng các quy tắc giao hoán, kết hợp, và phân phối của đại số (cùng với định nghĩa i² - 1); như sau:

• cộng - addition: (x+iy) + (v+iw) = (x+v) + i(y+w).
• nhân - multiplication: (x + iy) * (v + iw) = (xv - yw) + i(yv + xw).
• mô đun - magnitude: |x + iy| = sqrt(x^2 + y^2)
• phần thực và phần ảo: re(x + iy) = x, và im(x + iy) = y

Với các định nghĩa cơ bản trên, cách cài một cấu trúc dữ liệu cho số phức rất rõ ràng. Ta bắt đầu bằng một API quy định các thao tác của kiểu dữ liệu:

Code cài đặt các phương thức số học sử dụng một cơ chế mới cho việc truy nhập các giá trị của đối tượng:

• Truy nhập dữ liệu của các đối tượng cùng kiểu. Cả plus() và times() cần truy nhập dữ liệu của hai đối tượng: đối tượng được truyền vào dưới dạng tham số và đối tượng dùng để gọi phương thức. Nếu phương thức được gọi bằng lệnh a.plus(b). như thường lệ, ta có thể truy nhập dữ liệu của a bằng cách gọi tên các biến thực thể re và im, nhưng để truy nhập vào dữ liệu của b ta dùng cách b.re và b.im. Tuy nhiên, do ta đã quy định các biến thực thể là private, ta không thể truy nhập trực tiếp các biến thực thể của các đối tượng thuộc class khác (nhưng ta có thể truy nhập các đối tượng thuộc cùng một class hiện tại). Chính sách này giảm độ linh hoạt nhưng tăng chất lượng thiết kế khi ta phát triển các chương trình có nhiều mô đun.
• Gọi hàm thành chuỗi. Hãy quan sát cách hàm main() nối hai lời gọi hàm thành một biểu thức: biểu thức z.times(z).plus(z0) cho kết quả bằng z² + z0. Cách sử dụng này rất thuận tiện vì ta không phải tạo thêm một biến để giữ giá trị trung gian. Nếu bạn đọc kĩ biểu thức trên, bạn có thể thấy ngữ nghĩa rất rõ ràng: đọc từ trái sang phải, mỗi phương thức trả về tham chiếu tới một đối tượng Complex, tham chiếu đó được dùng để gọi phương thức tiếp theo. Nếu muốn, ta có thể dùng ngoặc để áp đặt thứ tự tính toán (chẳng hạn, z.times(z.plus(z0)) có nghĩa z(z + z0)).
• Tạo và trả về đối tượng mới. Hãy quan sát cách plus() và times() trả kết quả về cho client: chúng cần trả về một giá trị Complex, do đó mỗi hàm tính phần thực và phần ảo rồi dùng các kết quả đó để tạo đối tượng mới, cuối cùng trả về tham chiếu tới đối tượng mới đó. Cách làm này cho phép client xử lý các số phức bằng cách thao tác với các biến địa phương thuộc kiểu Complex.

Mandelbrot set.

Quy tắc xác định xem một số phức z0 có nằm trong tập Mandelbrot hay không rất đơn giản. Xét chuỗi số phức z0, z1, z2, ..., zi, ..., trong đó z_i+1 = (z_i)² + z0. Ví dụ, bảng dưới đây liệt kê những phần tử đầu tiên trong chuỗi tương ứng với z0 = 1 + i:

Kiểm tra xem một số phức có thuộc tập hợp hay không Trong một số trường hợp, ta có thể chứng minh các số có nằm trong tập hợp hay không. Ví dụ, 0 + 0i chắc chắn thuộc tập hợp (do mô đun (magnitude) của tất cả các số trong chuỗi của nó đều bằng 0), và 2 + 0i chắc chắn không thuộc tập hợp (vì chuỗi của nó chứa các lũy thừa của 2, nghĩa là không hội tụ). Cho một điểm phức, ta có thể tính các số hạng ở đầu chuỗi, nhưng có thể không thể biết chắc chuỗi đó có bị chặn hay không. Có một phép kiểm tra đảm bảo rằng một điểm không thuộc tập hợp: nếu mô đun của một số bất kì trong chuỗi lớn hơn 2 (ví dụ 3 + 0i) thì chuỗi đó chắc chắn không hội tụ.

Vẽ tập Mandelbrot. Dễ xác định biểu diễn hình ảnh của tập Mandelbrot. Cũng như khi vẽ một hàm số thực ta vẽ các điểm nằm trong một khoảng, ta vẽ tập Mandelbrot cũng bằng cách vẽ các điểm phức. Mỗi số phức x + iy ứng với một điểm (x,y) trên mặt phẳng, cho nên ta có thể vẽ kết quả như sau: Với một độ phân giải N cho trước, ta xác định một lưới đều đặn N x N điểm ảnh bên trong một hình vuông cho trước và vẽ một điểm ảnh màu đen nếu điểm tương ứng thuộc tập Mandelbrot, vẽ một điểm trắng nếu không phải. Hình vẽ này là một dạng mẫu kì lạ, với tất cả các điểm đen nối với nhau và rơi vào khu vực vuông 2 x 2 với tâm là điểm -1/2 + 0i. Với các giá trị lớn hơn của N, ta sẽ có các hình ảnh với độ phân giải cao hơn, với cái giá là nhiều phép tính toán hơn. Nhìn kĩ sẽ thấy những dạng đệ quy trên khắp hình vẽ. Ví dụ, hình bầu tròn với những cái mấu hình dáng tương tự mọc xung quanh xuất hiện ở khắp đường viền của khu vực đen chính. Khi ta phóng to vùng gần mép của hình xoắn, xuất hiện những hình xoắn tương tự!

Chương trình Mandelbrot.java dùng phép kiểm tra này để vẽ biểu diễn hình ảnh của tập Mandelbrot. Do kiến thức của ta về tập này không hẳn đen và trắng, ta dùng các sắc độ xám để biểu diễn. Chương trình dựa vào hàm dưới đây (một client của Complex), nó tính chuỗi xuất phát từ một số cho trước và trả về số vòng lặp mà trong đó mô đun không chạm đến 2, tính đến một số lần lặp tối đa:

public static int mand(Complex z0, int d) { Complex z = z0; for (int t = 0; t < d; t++) { if (z.abs() >= 2.0) return t; z = z.times(z).plus(z0); } return d; }

Với mỗi điểm, phương thức main() trong chương trình Mandelbrot tính điểm z0 ứng với điểm ảnh và tính 255 - mand(z0, 255) đại diện cho giá trị độ xám của điểm ảnh. Một điểm ảnh bất kì không phải màu đen ứng với một điểm mà ta biết là không nằm trong tập Mandelbrot, vì mô đun của các số trong chuỗi của nó vượt quá 2 (và do đó sẽ đi đến vô cùng); các điểm ảnh đen (độ xám 0) ứng với những điểm mà ta cho là thuộc tập Mandelbrot, vì mô đun nhỏ hơn 2 trong 255 lần lặp, nhưng ta không biết chắc. Độ phức tạp của các hình ảnh mà chương trình này tạo ra khá là ấn tượng, ngay cả khi ta phóng to một mẩu nhỏ xíu trên mặt phẳng. Để có các hình ảnh ấn tượng hơn nữa, ta có thể dùng mầu (xem bài tập 3.2.33)

Q + A (Hỏi + Đáp)

Q. Biến thực thể có giá trị khởi tạo sẵn hay không?

A. Có. Chúng tự động có giá trị bằng 0 đối với các kiểu số, false đối với kiểu boolean, và giá trị đặc biệt null đối với tất cả các kiểu tham chiếu.

Q. null là gì?

A. Nó là một giá trị với nghĩa là không chiếu tới đối tượng nào. Dùng tham chiếu null để gọi một phương thức là việc làm vô nghĩa và sẽ gây ra lỗi NullPointerException.

Q. Ta có thể khởi tạo các biến thực thể khi khai báo chúng hay không?

A. Có, bạn có thể khởi tạo các biến thực thể tương tự với cách khởi tạo biến địa phương. Mỗi lần một đối tượng được client tạo bằng toán tử new, các biến thực thể của nó sẽ được khởi tạo bằng chính các giá trị đó, sau đó constructor mới được gọi.

Q. Class nào cũng phải có một constructor?

A. Đúng vậy, nhưng nếu bạn không định nghĩa một constructor nào, Java sẽ tự động cung cấp một constructor mặc định (không có tham số). Khi client gọi constructor với lệnh new, các biến thực thể được khởi tạo như bình thường. Nếu bạn định nghĩa một constructor, Java sẽ không cung cấp constructor mặc định nữa.

Q. Nếu như trong class không có hàm toString(). Chuyện gì xảy ra nếu tôi muốn in một đối tượng thuộc kiểu đó với lệnh StdOut.println()?

A. Kết quả in ra sẽ là một số nguyên: hash code của đối tượng. Phần lớn các class không cài hàm toString() hay hàm hashCode(). Giá trị mặc định thu được thường là kết quả của việc biến đổi địa chỉ bộ nhớ của đối tượng ra dạng số nguyên.

Q. Bên trong class cài đặt một cấu trúc dữ liệu có được có một hàm static không?

A. Tất nhiên là có. Tất cả các lớp ta đã viết đều có hàm main(). Nhưng rất dễ nhầm lẫn khi trong một class có cả các phương thức static lẫn các phương thức thực thể. Ví dụ, người ta hay dùng các phương thức static cho các thao tác xử lý cùng lúc nhiều đối tượng, mà trong đó không có đối tượng nào nên giữ vai trò chính: dùng để gọi hàm. Ví dụ, ta gọi z.abs() để lấy giá trị của |z|, nhưng gọi a.plus(b) để lấy tổng thì có lẽ không tự nhiên lắm. Tại sao không phải là b.plus(a)? Một lựa chọn khác là định nghĩa một hàm static bên trong Complex, chẳng hạn

public static Complex plus(Complex a, Complex b) { return new Complex(a.re + b.re, a.im + b.im); }

z = z.times(z).plus(z0).

z = Complex.plus(Complex.times(z, z), z0)

Q. Các phép tính toán plus() và times() trông có vẻ khá là vụng về. có cách nào sử dụng kí hiệu kiểu như * và + trong các biểu thức chứa các đối tượng như Complex và Vector, để ta có thể viết biểu thức như z = z * z + z0 ?

A. Một số ngôn ngữ (nổi bật nhất là C++) hỗ trợ tính năng này, nó được gọi là operator overloading - cài chồng toán tử, nhưng Java thì không (ngoại trừ phép + với nghĩa nối xâu kí tự). Như thường lệ, đây là quyết định của người thiết kế ngôn ngữ, và ta không có cách nào khác là chấp nhận. Nhưng nhiều lập trình viên Java không coi đây là sự thiếu hụt. Việc cài chồng toán tử chỉ có ý nghĩa đối với các kiểu biểu diễn số hoặc các trừu tượng đại số, vốn chỉ chiếm một phần rất nhỏ trong tổng thể các cấu trúc dữ liệu. Và nhiều chương trình sẽ dễ hiểu hơn khi các toán tử có tên mang tính mô tả, chẳng hạn như plus và times.

Q. Trong class còn có loại biến nào khác ngoài tham số, biến địa phương và biến thực thể?

A. Nếu bạn dùng từ khóa static trong khai báo biến, nó sẽ tạo ta một kiểu biến hoàn toàn khác, được gọi là static variable - biến của class. Các biến static cũng được truy nhập từ bất cứ phương thức nào trong class, tuy nhiên, chúng không gắn với bất kì đối tượng nào. Trong những ngôn ngữ lập trình cổ hơn, những biến như vậy được xem là các biến toàn cục - global variables, vì phạm vi toàn cục của nó. Trong lập trình hiện đại, ta chú trọng vào việc giảm phạm vi, và do đó ít khi sử dụng những biến như vậy.

Q. Có quan hệ gì giữa lớp Vector trong mục này với Vector trong thư viện Java?

A. Không, ta dùng cái tên đó vì vector là thuật ngữ của ngành vật lý và đại số.

Q. Mandlebrot tạo ra hàng trăm triệu đối tượng Complex. Việc tạo ra tất cả đống đối tượng đó có làm chậm chương trình?

A. Đúng là có, nhưng không đến nỗi làm ta không thể tạo ra hình vẽ. Mục tiêu của ta là làm cho chương trình dễ đọc dễ hiểu và dễ bảo trì - việc dùng cấu trúc Complex để giảm phạm vi đã giúp ta đạt được mục đích đó. Chắc chắn bạn có thể tăng tốc độ Mandelbrot bằng cách không sử dụng cấu trúc Complex hoặc bằng một cài đặt khác của Complex.

Q. Thông báo lỗi "can't make a static reference to a non-static variable" nghĩa là gì?

A.

public class Test { private static int M; // class variable private int N; // instance variable public static int getM() { return M; } // OK public static int getN() { return N; } // ERROR }

Bài tập

1. Tại sao chương trình Bug1.java gây lỗi java.lang.NullPointerException khi chạy?

   public class Bug1 { private String s; public void Bug1() { s = "hello"; } public String toString() { return s.toUpperCase(); } public static void main(String[] args) { Bug1 x = new Bug1(); StdOut.println(x); } }

   Trả lời: lập trình viên có lẽ định cho constructor không có tham số gán cho s giá trị hello. Tuy nhiên, hàm Bug1() lại có một kiểu trả về là (void) nên nó chỉ là một phương thức thực thể thông thường tình cờ trùng tên với tên class, chứ không phải một constructor.

2. Tại sao chương trình Bug2.java gây lỗi java.lang.NullPointerException khi chạy?
3. Cài một cấu trúc dữ liệu Die để thả xúc xắc chuẩn với 6 mặt. Class Die có một phương thức roll() có nhiệm vụ thả và sửa giá trị xúc xắc thành giá trị vừa thả được, và một hàm lấy giá trị value.
4. Cài một cấu trúc dữ liệu biến đổi cho thanh ghi LFSR (linear feedback shift register).
5. Cài một cấu trúc dữ liệu biến đổi Counter (con đếm).
6. Cài một cấu trúc dữ liệu biến đổi Odometer.
7. Cài một cấu trúc dữ liệu biến đổi StopWatch.
8. Cài một cấu trúc dữ liệu VotingMachine phục vụ bỏ phiếu bầu cử. trong đó có các phương thức làm thay đổi trạng thái voteRepublican(), voteDemocrat(), và voteIndependent(). một phương thức đọc trạng thái getCount() trả về tổng số phiếu đã bỏ.
9. Chuyện gì xảy ra nếu bạn dịch và chạy đoạn code sau?

   Student x; StdOut.println(x);

   Trả lời: có lỗi biên dịch x có thể chưa được khởi tạo.

10. Giả sử bạn muốn thêm một constructor vào Complex, constructor mới lấy một đối số real và khởi tạo một đối tượng Complex với giá trị đó. Bạn viết đoạn mã sau

    public void Complex(double real) { re = real; im = 0.0; }

    Tại sao lệnh Complex c = new Complex(1.0) gây lỗi biên dịch? Trả lời: các constructor không có kiểu trả về, thậm chí không có cả void. Cho nên đoạn trên thực ra là một phương thức có tên Complex chứ không phải constructor. Xóa từ khóa void và chương trình sẽ chạy. Đây là mẹo lừa thường gặp.

11. Chuyện gì xảy ra nếu bạn dịch và chạy đoạn code sau?

    Student[] students = new Student[10]; StdOut.println(students[5]);

    Trả lời: Nó dịch được và in ra null.

12. Đoạn sau có lỗi gì?

    int N = 17; Dog[] dogs = new Dog[N]; for (int i = 0; i < N; i++) { dog.bark(); dog.eat(); }

    Trả lời: nó gây lỗi NullPointerException vì ta quên dùng new để tạo từng đối tượng Dog. Để sửa lỗi, thêm vòng lặp sau vào sau lệnh khởi tạo mảng.

    for (int i = 0; i < N; i++) dogs[i] = new Dog();

13. Đoạn sau in ra gì?

    Complex c = new Complex(2.0, 0.0); StdOut.println(c); StdOut.println(c.mul(c).mul(c).mul(c)); StdOut.println(c);

14. Sửa phương thức toString trong file Complex.java để nó in 3 - i thành 3 - i thay vì of 3 + -i, và in 3 thành 3 thay vì 3 + 0i.
15. Có gì sai trong đoạn code hoán đổi giá trị giữa các đối tượng Student x và y dưới đây?

    Student swap = new Student(); swap = x; x = y; y = swap;

    Trả lời: Đầu tiên, Student không có constructor không lấy tham số. Nếu có, đoạn code trên đúng về kĩ thuật, nhưng lệnh new Student() không cần thiết và phí phạm. Nó cấp phát bộ nhớ cho một đối tượng Student mới, chiếu swap tới đối tượng mới đó, rồi ngay sau đó chiếu swap tới x. Đối tượng vừa được cấp phát không thể được truy nhập đến nữa. Phiên bản sau đúng.

    Student swap = x; x = y; y = swap;

16. Thêm phương thức minus(Complex b) vào class Complex, phương thức này lấy một tham số b kiểu Complex và trả về hiệu của đối tượng gọi hàm trừ đi b.
17. Thêm phương thức divides(Complex b) vào class Complex, phương thức này lấy một tham số b kiểu Complex và trả về kết quả phép chia của đối tượng gọi hàm chia cho b.
18. Thêm phương thức conjugate() vào class Complex trả về liên hợp phức (complex conjugate) của đối tượng gọi hàm.
19. Viết chương trình RootsOfUnity.java nhận N là tham số dòng lệnh và dùng lớp Complex để tính và in ra N căn bậc N của đơn vị.
20. Write a program to read in three real numbers a, b, and c and print out all roots of ax² + bx + c, including complex ones.
21. Find inputs to the Mandelbrot update formula that make it converge (z0 = 1/2 + 0i), cycle with a period of 1 (z0 = -2 + 0i), cycle with a period of 2 (z0 = -1 + 0i), or stay bounded without converging (z0 = -3/2 + 0i).
22. Viết chương trình ColorMandelbrot.java vẽ một phiên bản có màu của tập Mandelbrot set. Đọc từ input chuẩn một mảng 256 dòng 3 cột sau đó khi vẽ dùng mầu thứ i nếu hàm Mandelbrot chạy i lần lặp. Dùng file dữ liệu mandel.txt làm một ví dụ.

    -1.5 -1.0 2.0 2.0		0.10259 -0.641 0.0086 0.0086

23. Tập Julia. Tập Julia của một số phức cho trước là một tập điểm liên quan đến hàm Mandelbrot. Thay vì cố định z và cho c thay đổi, ta cố định c và cho z thay đổi. Tập Julia là tập các điểm z mà hàm Mandelbrot sửa đổi bị chặn; các điểm mà chuỗi không hội tụ không thuộc tập này. Tất cả các điểm z được quan tâm đều nằm trong hình vuông 4x4 với tâm tại gốc tọa độ. Tập Julia cho c liên thông khi và chỉ khi c nằm trong tập Mandelbrot! Viết chương trình ColorJulia.java lấy hai tham số dòng lệnh a và b, và dùng màu để vẽ tập Julia cho c = a + ib. Đọc từ input chuẩn một mảng mầu gồm 256 dòng 3 cột và dùng màu thứ i nếu hàm Julia chạy i lần lặp. Dùng file dữ liệu mandel.txt làm ví dụ.

    -1.25 0.00		-0.75 0.10

24. Point3D. Tạo một cấu trúc dữ liệu cho các điểm trong một không gian 3 chiều. Class này có một constructor lấy 03 tọa độ thực x, y, và z; các phương thức distance, distanceSquared, và distanceL1 để tính khoảng cách Ơ-clit, bình phương khoảng cách Ơ-clit, và khoảng cách L1 (L1-distance - khoảng cách nếu lúc nào cũng đi song song với một trong ba trục tọa độ) tới gốc tọa độ.
25. Interval. Tạo một cấu trúc dữ liệu Interval.java biểu diễn các khoảng trên trục x. Một khoảng (interval) là một tập các điểm nằm trong khoảng [left, right]. một constructor có kiểm tra để đảm bảo điểm left không vượt quá điểm right; một phương thức intersects sao cho a.intersects(b) trả về true nếu khoảng a và khoảng b có phần chung, nếu không thì trả về false.
26. Tạo một cấu trúc dữ liệu PhoneNumber.java biểu diễn một số điện thoại Mỹ. Constructor cần lấy 3 tham số kiểu string: area code (gồm 3 chữ số), exchange (gồm 3 chữ số), và extension (4 chữ số). Phương thức toString trả về biểu diễn dạng String có dạng (800) 867-5309. (area code) exchange - extension. Phương thức equals sao cho p.equals(q) trả về true nếu hai số điện thoại p và q giống nhau, nếu không thì trả về false.
27. Làm lại PhoneNumber.java nhưng dùng ba biến thực thể là số nguyên. Cho constructor lấy tham số là các số nguyên. Hãy nhận xét về ưu nhược điểm của cách này so với cách dùng String.

    Trả lời: hiệu quả hơn về thời gian và bộ nhớ. nhưng phức tạp hơn khi phải xử lý các chữ số 0 ở hàm toString.

Bài tập sáng tạo

1. IP addresses - địa chỉ IP. Tạo một cấu trúc dữ liệu để biểu diễn các địa chỉ IPv4 (Internet Protocol, version 4). Một địa chỉ IP là một số nguyên 32 bit.
2. Dates - ngày. Tạo một cấu trúc dữ liệu kiểu Date biểu diễn một ngày. Bạn cần tạo được một đối tượng Date mới từ các giá trị month, day, và year. Cấu trúc này cần hỗ trợ các phương thức tính số ngày là khoảng cách giữa hai Date, trả về thứ của một Date, v.v..
3. Time bombs - Bom hẹn giờ UNIX biểu diễn date bằng một số nguyên có dấu là số giây tính từ ngày 1 tháng 1 năm 1970. Viết một chương trình client tính represents the date with a signed integer measuring the number of seconds since January 1, 1970. Write a client program to calculate when this date will occur. Add a static method add(Date d, int days) to your date data type that returns a new date which is the specified number of days after the date d. Note that there are 86,400 seconds in a day.
4. Qubits. In quantum computing, a qubit plays the role of a bit. It is a complex number a + bi such that |a + bi| = 1. Once we measure a qubit, it "decides" to be a 1 with probability a² and a 0 with probability b². Any subsequent observations will always yield the same value. Implement a data type Qubit that has a constructor Qubit(a, b) and a boolean method observe that returns true or false with the proscribed probabilities.
5. Biorhythms. A biorhythm is a pseudo-scientific profile of the three natural cycles of your body: physical (23 days), emotional (28 days), and intellectual (31 days). Write a program that takes six command line inputs M, D, Y, m, d, and y where (M, D, Y) is the month (1-12), day (1-31), and year (1900-2100) of your birthday and (m, d, y) is today's month, day, and year. It should then print out your biorhythm on a scale of -1.0 to 1.0 according to the formula: sin (2 π age / cycle length). Use the date data type created in the previous exercise.
6. Particle. Create a data type for elementary or composite particles (electron, proton, quark, photon, atom, molecule). Each particle should have an instance variable to store its name, its mass, its charge, and its spin (multiple of 1/2).
7. Quark. Quarks are the smallest known building blocks of matter. Create a data type for quarks. Include a field for its type (up, down, charm, strange, top, or bottom) and its color (red, green, or blue). The charges are +2/3, -1/3, +2/3, -1/3, +2/3, -1/3, respectively. All have spin 1/2.

   Diffusion of particles in a fluid.

   Simulate diffusion of particles in a fluid. See BrownianParticle.java in Section 9.8.
8. Biorhythms. Plot your biorhythm in turtle graphics over a 6 week interval. Identify critical days when your rhythm goes from positive to negative - according to biorhythm theory, this is when you are most prone to accident, instability, and error.
9. Vector3. Include normal vector operations for 3-vectors, including cross product. The cross product of two vectors is another vector. a cross b = ||a|| ||b|| sin(theta) n, where theta is angle between a and b, and n is unit normal vector perpendicular to both a and b. (a₁, a₂, a₃) cross (b₁, b₂, b₃) = (a₂ b₃ - a₃ b₂, a₃ b₁ - a₁ b₃, a₁ b₂ - a₂ b₁). Note that |a cross b| = area of the parallelogram with sides a and b. Cross product arises in definition of torque, angular momentum and vector operator curl.
10. Four-vector. Create a data type for four-vectors. A four-vector is a four-dimensional vector (t, x, y, z) subject to Lorentz transformations. Useful in special relativity.
11. Euclidean points. Create a data type EuclideanPoint.java that represents a d-dimensional point. Include a method so that p.distanceTo(q) returns the Euclidean distance between points p and q.
12. Vector field. A vector field associates a vector with every point in a Euclidean space. Widely used in physics to model speed and direction of a moving object or or strength and direction of a Newtonian force.
13. Soda machine. Create a data type SodaMachine that has methods insertCoin(), getChange(), buy(), etc.
14. Months. Write a data type Month that represents one of the twelve months of the year. It should have fields for the name of the month, the number of days in the month, and the birthstone.

    MONTH	DAYS	BIRTHSTONE
    January	31	Garnet
    February	28	Amethyst
    March	31	Aquamarine
    April	30	Diamond
    May	31	Emerald
    June	30	Alexandrite
    July	31	Ruby
    August	31	Peridot
    September	30	Sapphires
    October	31	Opal
    November	30	Topaz
    December	31	Blue Zircon

    
    

15. Chaos with Newton's method. The polynomial f(z) = z⁴ - 1 as 4 roots at 1, -1, i, and -i. We can find the roots using Newton's method over the complex plane: z_k+1 = z_k - f(z_k)/f'(z_k). Here f(z) = z⁴ - 1 and f'(z) = 4z³. The method converges to one of the 4 roots depending on the starting point z_0. Choose each point in the complex plane with coordinates between -1 and 1 and determine which of the four roots it converges to, and plot the point either white, red, green, or blue accordingly. If Newton's method doesn't converge after 100 iterations, color the point black. Name your program NewtonChaos.java.
    

16. Gauss multiplication. Implement complex multiplication using only 3 floating point multiplications (instead of 4). You may use as many as 5 floating point additions. Answer: Gauss gave the following method to multiply (a + bi)(c + di). Set x1 = (a + b)(c + d), x2 = ac, x3 = bd. Then the product is given by x + yi where x = x2 - x3, y = x1 - x2 - x3.
17. Rational numbers. Create a data type Rational.java and BigRational.java for positive rational numbers.
18. Rational numbers. Modify Rational.java to provide support for negative rationals and zero.
19. Quaternions. In 1843, Sir William Hamilton discovered an extension to complex numbers called quaternions. Quaternions extend the concept of rotation in three dimensions to four dimensions. They are used in computer graphics, control theory, signal processing, and orbital mechanics, e.g., command for spacecraft attitude control systems. are related to Pauli spin matrices in physics. Create a date type Quaternion.java to represent quaternions. Include operations for adding, multiplying, inverting, conjugating, and taking the norm of quaternions.

    A quaternion can be represented by a 4-tuple of real numbers (a0, a1, a2, a3), which represents a0 + a1 i + a2 j + a3 k. The funadmental identity is i^2 = j^2 = k^2 = ijk = -1. The quaternion conjugate is (a0, -a1, -a2, -a3). The quaternion norm is sqrt(a0² + a1² + a2² + a3²). The inverse of a quaternion is (a0/d, -a1/d, -a2/d, -a3/d) where d is the square of the quaternion norm. The sum of two quaternions (a0, a1, a2, a3) and (b0, b1, b2, b3) is (a0+b0, a1+b1, a2+b2, a3+b3), the product is (a0b0 - a1b1 - a2b2 - a3b3, a0b1 + a1b0 + a2b3 - a3b2, a0b2 - a1b3 + a2b0 + a3b1, a0b3 + a1b2 - a2b1 + a3b0), and the quotient a/b is the product of (a0, a1, a2, a3) and the inverse of (b0, b1, b2, b3). Note that ab doesn't equal ba in general.

20. Equipotential surfaces. An equipotential surface is the set of all points that have the same electric potential V. Given a group of N point charges, it is useful to visualize the electric potential by plotting equipotential surfaces (aka countour plots). Program Equipotential.java draws a line every 5V by computing the potential at each gridpoint and checking whether the potential is within 1 pixel of a multiple of 5V. Since the electric field E measures how much the potential changes, E * eps is the range that the potential changes in a distance of 1 pixel.

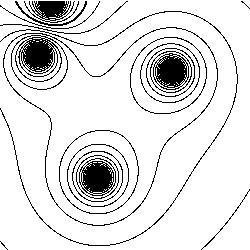
    It is also interesting to plot the field lines and the equipotential lines simultaneously. The field lines are always perpendicular the the equipotential lines.

21. Tensors. Create a data type for tensors.
22. UN Countries. Create a data type Countryfor UN countries. Include fields for 3 digit UN Code, 3 letter ISO abbreviation, country name, and capital. Write a program Country.java that reads in a list of countries and stores them in an array of type Country. Use the method String.split to help parse the input file.
23. Area codes. Create a data type for telephone area codes in North America. Include fields for the area code, the city, and state, and the two letter state abbreviation. Or for international phone codes. Include a field for zone, code, and country.
24. Congressional districts. Create a data type for places, counties, and congressional districts. Include fields for place name, county name, county code, zip code, congressional district, etc. Use the data sets from the 1998 FIPS55-DC3 Index: Pennsylvania (2MB) or all 50 states plus DC and 9 outlying areas (30MB).
25. Latitudes and longitudes. For USA latitudes and longitudes, use the TIGER database or www.bcca.org or gazetteer. For the rest of the world, use earth-info.
26. Astronomy. Data for asteroids, meteors, and comets.
27. Fortune 1000 companies. Create a data type the for Fortune 1000. Include fields for company name and sales revenue in millions of dollars. Data taken from April 15, 2002 issue of Fortune. Note: currently need to parse data.
28. Elements. Create a data type Element.java for the Periodic Table of Elements. Include fields for element, atomic number, symbol, and atomic weight. (Ignore fields for boiling point, melting point, density (kg/m3), Heat vapour (kJ/mol), heat fusion (kJ/mol), thermal conductivity (W/m/K), and specific heat capacity (J/kg/K) since it's not know for all elements). The file is in CSV format (fields separated by commas).
29. Molecular weight. Write a program so that the user enters a molecule H2 O and the program calculates its molecular weight.
30. Some potentially useful datafiles: aroma therapies, nutritional information, meteorological glossary, psychiatric disorders, words translated in 15 languages, dictionary of emoticons, meanings of common names, World Almanac facts about countries.

31. Student records. Create a data type Student.java to represent students in an introductory computer science course. Each student record object should represent a first name, last name, email address, and section number. Include a toString() method that returns a string representation of a student and a less() method that compares two students by section number. To do so, implement the following API:

    public class Student -------------------------------------------------------------------------- public Student(String first, String last, String email, int section) public boolean less(Student s2) // true if this student's section is smaller than that of s2 String toString() // string representation of student (section, first name, last name, and email)

32. Impedance. Impedance is the generalization of resistance from DC circuits to AC circuits. In an AC circuit, the impedance of a component measures its opposition to the flow of electrons at a given frequency ω. The impedance has two components: the resistance and the reactance. The resistance R of a circuit component measures its opposition to the movement of electrons (friction against motion of electrons) when a given voltage is applied. The reactance X of a circuit component measures its ability to store and release energy as the current and voltage fluctuate (inertia against motion of electrons).

    In circuits with resistors only, the current is directly proportional to the voltage. However, with capacitors and inductors, there is a +- 90 degree "phase shift" between the current and voltage. This means that when the voltage wave is at its maximum, the current is 0, and when the current is at its maximum the voltage is 0. To unify the treatment of resistors (R), inductors (L), and capacitors (C) it is convenient to treat the impedance as the complex quantity Z = R + iX. the impedance of an inductor is iwL and the impedance of a capacitor is 1/iwC. To determine the impedance of a sequence of circuit elements in series, we simply add up their individual impedances. Two important quantities in electrical engineering are themagnitude of the impedance and the phase angle. The magnitude is the ratio of the RMS voltage to the RMS current - it equals the magnitude of the complex impedance. The phase angle is the amount by which the voltage leads or lags the current - it is the phase of the complex impedance. Program CircuitRLC.java does a computation involving complex numbers and impedance of circuits with resistors, inductors, and capacitors in series.

    Exercise: RLC circuit in parallel. 1/Z = 1/Z1 + 1/Z2 + ... 1/Zn.

    Exercise (for objects): repeat series-parallel network for RLC circuits with impedances instead of resistance

33. Diffusion of particles in a fluid. Simulate diffusion of particles in a fluid. See BrownianParticle.java in Section 9.8.
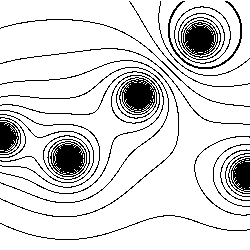
34. Electric field lines. Michael Faraday introduced an abstraction called electric field lines to visualize the electric field. By Coulombs law, the electric field at a point induced by a point charge q_i is given by E_i = k q_i / r², and the direction points to q_i if q_i is negative and away from q_i it is positive. If there are a group of n point charges, the electric field at a point is the vector sum of the electric fields induced by the n individual point charges. We can compute it by summing up the components in the x- and y- directions. The figure below illustrates the field lines for two equal positive point charges (left) and two point charges of opposite signs (right). The second configuration is called an electric dipole: the charges cancel each other out, and the electric field weakens very quickly as you move away from the charges. Examples of dipoles can be found in molecules where charge is not evenly distributed. Oscillating dipoles can be used to produce electromagnetic waves to transmit radio and television signals.

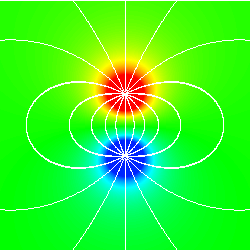
    Program FieldLines.java draws 10 electric field lines coming out of each charge. (We take some liberties since traditionally the number of field lines per unit area should be proportional to the magnitude of the field strength.) Each line starts on a 1-pixel circle around the charge, at twelve equally spaced angles. The electric field at a point (x, y) from a point charge q_i is given by E_i = k q_i / r², where q_i is the magnitude of the charge i and r is the radial distance from it. The field due to several charges is the vector sum of the field due to each, and can be found by adding the x- and y-components. After calculating the electric field strength, we move in the direction of the vector field and draws a spot. We repeat this process until we reach the boundary of the region or another point charge. The figures below illustrate the electric potential and field lines for several random charges of equal magnitude.

35. Koch snowflake with rainbow of colors.

    The Koch snowflake of order n consists of three copies of the Koch curve of over n. We draw the three Koch curves one after the other, but rotate 120° clockwise in between. Below are the Koch snowflakes of order 0, 1, 2, and 3. Write a program KochRainbow.java that plotsthe Koch snowflake in a continuous spectrum of colors from red, to orange, yellow, green, blue, and indigo, and violet.

36. Anti-Koch snowflakes. The anti-Koch snowflake is generated exactly like the Koch snowflake, except that clockwise and counterclockwise are interchanged. Write a program AntiKoch.java that takes a command line parameter N and plots the anti-Koch snowflake of order N using Turtle graphics.

37. Randomized Koch snowflakes. A randomized Koch snowflake is generated exactly like the Koch snowflake, except that we flip a coin to generate the clockwise and counterclockwise direction at each step.
38. Turtle graphics.
    1. Minkowski sausage. (Sausage.java)
    2. Gosper island.
    3. Cesaro broken square.
39. More turtle graphics. Write a program to produce each of the following recursive patterns.
    1. Levy tapestry. (Levy.java)
    2. Fudgeflake.
40. Turtle graphics (hard). Write a program to produce each of the following recursive patterns without lifting the pen or tracing over the same line segment more than once.
    1. Hilbert space-filling curve. (Hilbert.java or SingleHilbert.java) Informally, a space-filling curve is a continuous curve in the unit square that passes through every point. In 1890, Giuseppe Peano discovered the first such space-filling curve. In 1891, David Hilbert discovered a simpler version, which came to be known as the Hilbert curve.
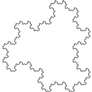
    2. Sierpinski arrowhead.
    3. Sierpinski curve.
41. Dragon curve. Write a program Dragon.java that reads in a command-line parameter N and plots the order N dragon curve using turtle graphics. The dragon curve was first discovered by three NASA physicists (John E. Heighway, Bruce A. Banks, and William G. Harter) and later popularized by Martin Gardner in Scientific American (March and April 1967) and Michael Crichton in Jurassic Park.

    This is a sophisticated program that uses two mutually recursive functions.

    Program SequentialDragon.java is an iterative version of the dragon curve. It is a hacker's paradise.

42. Mandelbrot trajectory. Write an interactive program Trajectory.java that plots the sequence of points in the Mandelbrot iteration in the complex plane. If the user clicks on (x, y), plot the sequence of iterates for z = x + iy.
43. Faster Mandelbrot. Speed up Mandelbrot by performing the computation directly instead of using Complex. Compare. Incorporate periodicity checking or boundary tracing for further improvements. Use divide-and-conquer: choose 4 corners of a rectangle and a few random points inside; if they're all the same color, color the whole rectangle that color; otherwise divide into 4 rectangles and recur.
44. More Complex methods. Add methods to Complex.java to support trigonometric and exponential functions on complex numbers.
    • exp(a + ib) = e^a cos(b) + i e^a sin(b)
    • sin(a + ib) = sin(a) cosh(b) + i cos(a) sinh(b)
    • cos(a + ib) = cos(a) cosh(b) - i sin(a) sinh(b)
    • tan(a + ib) = sin(a + ib) / cos(a + ib)
45. Add a method power to Complex so that a.power(b) returns the result of taking the complex number a and taking it to the complex power b.
46. What is the principle value of iⁱ?

    Answer: e^-Π/2 = 0.207879576....

47. Random walker. Write a data type RandomWalker that simulates the motion of a random walker in the plane that starts at the origin and makes a random step (left, right, up, or down) at each step. Include a method step() that moves the random walker one step and a method distance() that returns the distance the random walker is from the origin. Use this data type to formulate a hypothesis as to how far (as a function of N) the random walker is from the origin after N steps. (See also Exercise 1.x.)

48. Turtle graphics. Extend Turtle in various ways. Make DeluxeTurtle that adds color, etc. Add a version that supports error checking. For example, throw a TurtleOutOfBounds exception if turtle goes outside designated boundary.

Last modified on May 11, 2015.

Copyright © 2002–2012 Robert Sedgewick and Kevin Wayne. All rights reserved.